最长公共子序列

发表于   |  

定义

什么是最长公共子序列（LongestCommon Subsequence, LCS）?
一个序列S任意删除若干字符得到新序列T，则T叫做S的子序列。
两个序列X和Y的公共子序列中，长度最长的哪个，定义为X和Y的LCS

举个例子：
X：13455
Y：245576
T：4 5 5
T即是X和Y的最长公共子序列。

注意区别最长公共子串：最长公共子串要求连续。
如“acdfg”同“akdfc”的最长公共子串为“df”，而它们的LCS为“adf”

算法

穷举法

假定字符串 X,Y 的长度分别为 m，n
对X的每一个子序列，检查它是否也是Y的子序列，从而确定它是否为X和Y的公共子序列，并且在检查过程中选出最长的公共子序列。
时间复杂度为O(2m * 2n), 不可取。

动态规划

使用c[i,j]记录序列Xi和Yj的最长公共子序列的长度。
其中Xi表示序列X前i位的子序列。Yj同理。
当x=0或y=0时,空序列即是最长公共子序列。

故有如下递推关系：

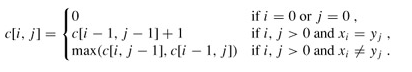
计算最长公共子序列长度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/******************************
X = "abcde"
Y = "bacdefa"
lx = X.length()
ly = Y.length()
c[lx+1][ly+1]
path[lx+1][ly+1]    //标记方向，取值为Left(1), Top(2), LeftTop(3)
*******************************/
Procedure LCS_LENGTH(X, Y) {
    // c[][], path[][] initial
    for (i = 0; i <= lx; i++) c[i][0] = 0;
    for (j = 0; j <= ly; j++) c[0][j] = 0;
    // i:列 j:行
    for (i = 1; i <= lx; i++) {
        for (j = 1; j <= ly; j++) {
            if (A[i-1] == B[j-1]) {
                c[i][j] = c[i-1][j-1] + 1;
                path[i][j] = 3;
            } else if (c[i][j-1] >= c[i-1][j]) {// if = ,generate several answers
                c[i][j] = c[i][j-1];
                path[i][j] = 2;
            } else {
                c[i][j] = c[i-1][j];
                path[i][j] = 1;
            }
        }
    }
    return(c, path);// the len of LCS is c[lx][ly]
}

构造最长公共子序列：

1
2
3
4
5
6
7
8
9
10
11
Procedure LCS(c, path, i, j) {
    if (i == 0 || j == 0) return;
    if (path[i][j] == 3) {
        LCS(b, path, i-1, j-1);
        print(A[i-1]);
    } else if (path[i][j] == 2){
        LCS(b, path, i, j-1);
    } else {
        LSC(b, path, i-1, j);
    }
}

练习

2015 算法 第二次练习
LCS 最长公共子序列问题

Problem A : Longest Common Subsequence From:UVA, 10405
读入两个字符串，输出最长公共子序列长度，模板题。
关键代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
while (in.hasNext()) {
    s1 = in.nextLine();
    s2 = in.nextLine();
    table = new int [s1.length()+1][s2.length()+1];

    for (int i = 1; i <= s1.length(); i++){
        for (int j = 1; j <= s2.length(); j++){
            if (s1.charAt(i-1) == s2.charAt(j-1)){
                table[i][j] = table[i-1][j-1] + 1;
            } else {
                table[i][j] = Math.max(table[i-1][j], table[i][j-1]);
            }
        }
    }
    System.out.println(table[s1.length()][s2.length()]);
}

Problem B : The Twin Towers ( From:UVA, 10066 )
思路同A题，只不过这题把字符串换成了整型数组，同样套模板。

Problem C : Vacatioui ( From:UVA, 10192 )
思路同A题。

Problem D : Compromise ( From:UVA, 531 )
首先要读入数据，将多行拼接成一个字符串，每行间添加一个空格，得到两个字符串。
将两个字符串用空格分割为两个字符串数组。（JAVA中可以使用String.split(“ “)）
根据递推得到最长公共子序列长度，同时（可以使用数组（使用不同数字代表方位））记录路径，
然后从最后一个递推之前的单词，加入ArrayList
输出

Problem E : Longest Match ( From:UVA, 10100 )
每组数据读入两个字符串
对于空行进行特判
对每个字符串将非字母数字的字符转换为空格
然后转化为字符串数组(split)
使用模板，输出
注意，输出中的 case 数宽度为 2

##参考

程序员编程艺术第十一章：最长公共子序列(LCS)问题